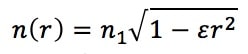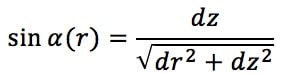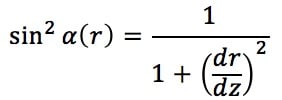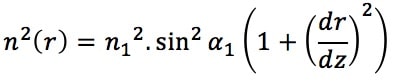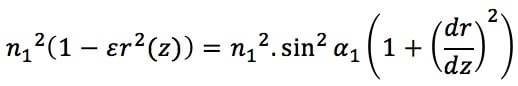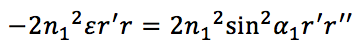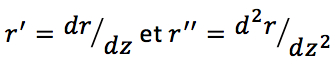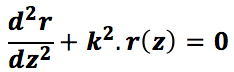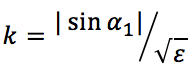Enoncé :
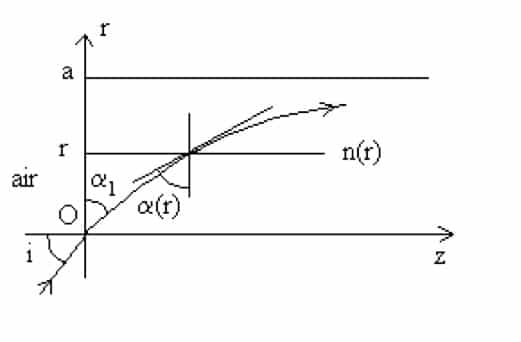
On considère un rayon lumineux incident provenant de l’air d’indice n1 et se propageant le long de l’axe des (z) à l’intérieur d’une fibre optique à gradient d’indice de diamètre a et d’indice :
avec ε>0, comme représenté sur la figure ci-dessous.
Le rayon incident fait un angle i avec l’axe (Oz) et l’on appelle α(r) l’angle que fait le rayon avec l’axe (Or) à une distance r de la base de la fibre.
Exprimer l’évolution du rayon en fonction de z, i.e. r(z).
Correction détaillée :
Il s’agit d’un exercice d’optique très classique, correspondant à la version continue d’une fibre optique à saut d’indice. Nous cherchons donc l’expression de r en fonction de z. Pour ce faire, nous devons trouver l’équation différentielle régissant l’évolution du rayon en fonction de l’altitude.
- Nous écrivons tout d’abord la loi de Descartes, en considérant une tranche {r;r+dr} de fibre optique, correspondant à une altitude {z;z+dz} ∶
Ce qui nous permet d’en déduire immédiatement :
- Nous avons fait apparaître un sinus, dont nous ne connaissons pas encore l’expression. Nous devons donc l’exprimer :
- Nous remarquons à ce stade qu’une dérivée de r en fonction de z commence à être mise en évidence. En effet, l’expression précédente se réécrit :
- En combinant ces équations, on en déduit finalement :
Soit:
Ce qui est bien une équation différentielle ne portant que sur r(z). Cependant, nous avons ici des termes au carré. L’idée est de dériver cette expression (méthode à retenir !) par rapport à z :
Où l’on a écrit :
- Evidemment, cette équation se simplifie grandement, et l’on obtient finalement :
où l’on a posé
L’exercice est donc résolu, cette équation étant celle d’un oscillateur harmonique simple.
En conclusion, cet exercice qui semble requérir beaucoup d’autonomie, n’est en réalité pas si complexe que cela : il suffit d’appliquer le cours et -il est vrai- d’être un peu astucieux… !
{loadposition auteur-olivier-malherbe}