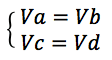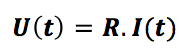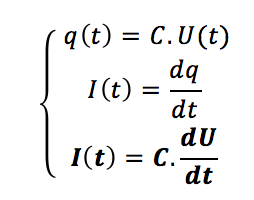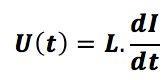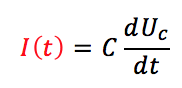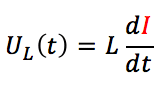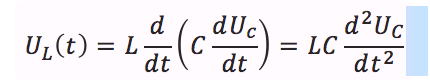Nous nous intéresserons ici uniquement à des considérations « macro » de l’électrocinétique, à savoir l’étude des circuits électriques à l’échelle des composants (résistance, condensateur, …) et pas le déplacement des charges à l’intérieur des fils.
Comprendre l’Approximation des Régimes Quasi Stationnaires (ARQS)
Vous en avez certainement souvent entendu parler, l’ARQS étant le cadre dans lequel s’étudient tous les problèmes d’électricité de sup. Se placer dans l’ARQS signifie tout simplement que l’on néglige le temps de propagation des charges à l’intérieur des fils électriques.
Pour illustrer très simplement cette approximation, cela consiste grossièrement à considérer que, lorsque vous appuyez sur un bouton pour allumer votre lampe, celle-ci s’allume instantanément (ce qui est en réalité faux puisque les charges ont nécessairement un certain temps de propagation). En termes formels, il faudra vérifier que la distance caractéristique du circuit est négligeable devant la longueur d’onde de l’onde étudiée.
Ne vous tracassez cependant pas plus que de raison avec l’ARQS : tous les problèmes d’électricité de sup se placent dans ce cadre, sans lequel par exemple la loi des nœuds n’est plus valable (cf équations de Maxwell).
Avant d’étudier un exemple, il faut absolument maîtriser quelques notions fondamentales.
Quelques considérations indispensables
1. La tension aux bornes d’un fil est nul
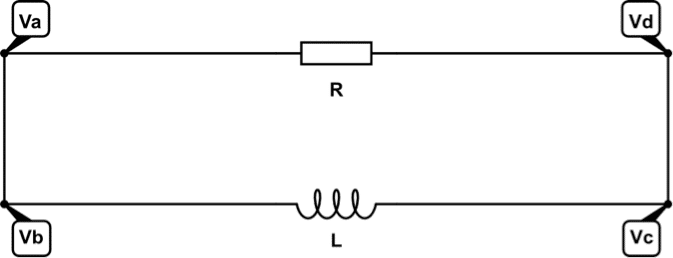
Il est absolument primordial de se souvenir qu’un potentiel se conserve le long d’un fil (tant que l’on ne rencontre pas de dipôle). Considérons le circuit simple suivant :
En appliquant ce qui a été précédemment dit, on a :
2. Connaître les principaux dipôles
Il est impératif de connaître sur le bout des doigts les quelques lois (simples) régissant l’évolution des principaux dipôles étudiés en sup, à savoir : la résistance, le condensateur et la bobine. Nous nous placerons toujours en convention récepteur.
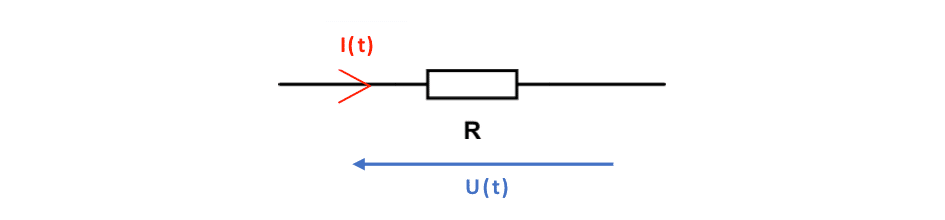
La résistance
Loi d’Ohm:
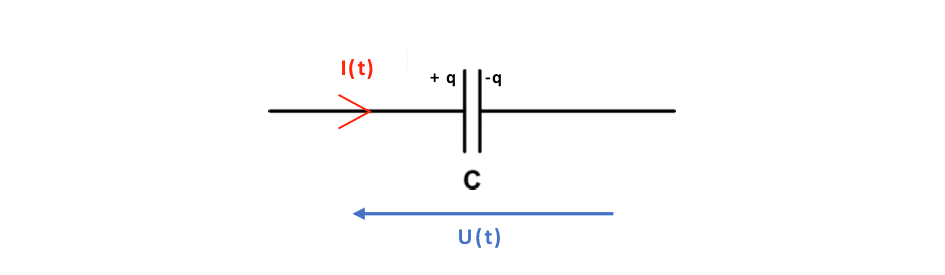
Le condensateur
Les deux premières équations permettent de trouver la troisième qui sera celle essentiellement utilisée dans les problèmes d’électricité.
Notez bien la disposition des charges +q et -q : si on les intervertit, des signes moins viennent modifier ces équations. Veillez donc bien à systématiquement garder cette convention.
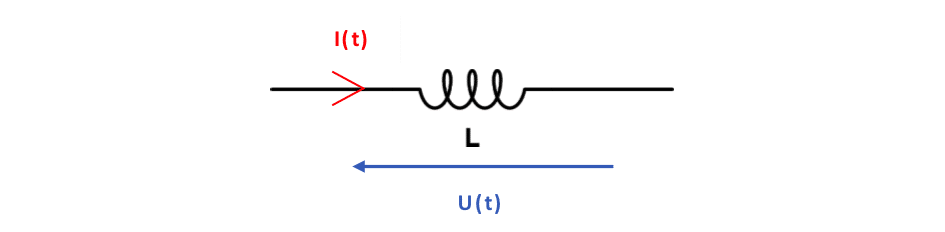
La bobine
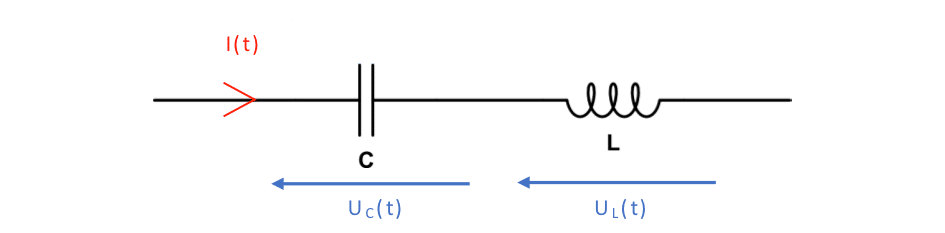
Ces relations constituent, avec les lois des mailles et des nœuds, l’essentiel de ce que vous avez à connaître en sup. Le principe est de combiner ces différentes équations : par exemple, pour une association en série d’un condensateur et d’une bobine, l’intensité I(t) traverse à la fois le condensateur et la bobine. Elle vérifie donc, grâce à son passage dans le condensateur :
et grâce à son passage dans la bobine :
On peut ainsi en déduire la relation :
Ces considérations, qui peuvent sembler très simples, constituent pourtant la base du raisonnement sur les circuits électriques : avoir la capacité (sans mauvais jeu de mot) de coupler les équations propres aux différents dipôles du circuit entre elles pour faire apparaître de nouvelles équations (différentielles en général).
3. Maîtriser la loi des nœuds et la loi des mailles
Un schéma vaut toujours mieux qu’un long discours.
Loi des mailles
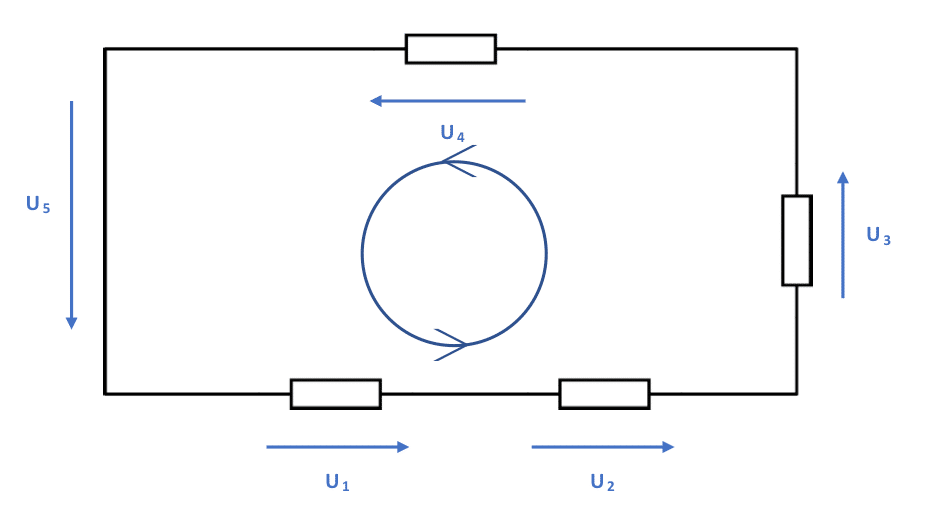
Sur le schéma ci-dessous, les « blocs » représentent des dipôles quelconques (pas nécessairement des résistances).
N.B : La tension U_5 ici n’est normalement pas représentée, puisque U_5=0 (tension aux bornes d’un fil). Elle est indiquée à titre pédagogique.
La loi des mailles s’écrit :
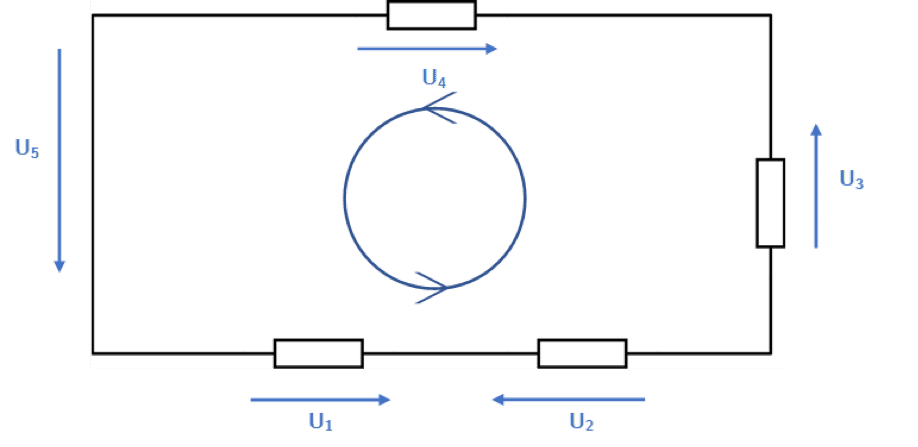
Il faut tout simplement sommer les tensions en longeant une maille, toujours dans le même sens. A titre d’exemple, considérons une nouvelle fois ce circuit, mais cette fois-ci changeons le sens des tensions U_2 et U_4 :
En tournant toujours dans le même sens, la loi des mailles s’écrit maintenant :
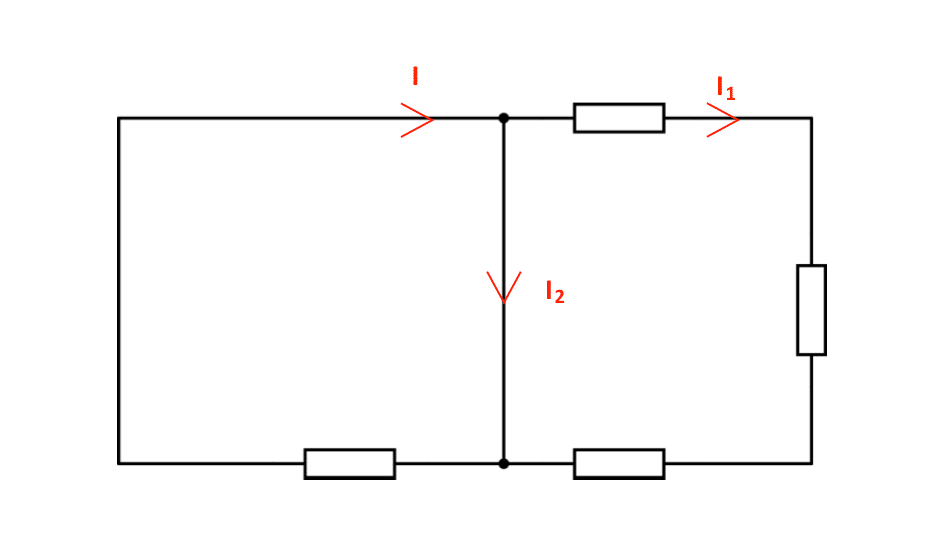
Loi des nœuds
La loi des nœuds s’écrit :
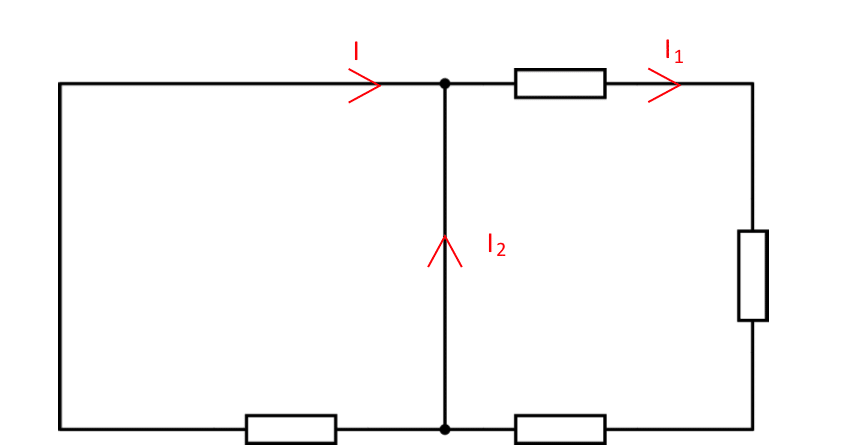
Si maintenant on appelle I_2 l’intensité considérée dans l’autre sens de propagation :
Alors cette fois-ci la loi des nœuds s’écrit :
La somme des intensités arrivant à un nœud est égale à la somme des intensités quittant ce nœud. Cela résume les outils indispensables à la résolution des exercices. Les autres formules (Millman, ponts diviseurs, etc) peuvent être utiles, mais elles dérivent toutes des formules ci-dessus et ne sont pas indispensables.