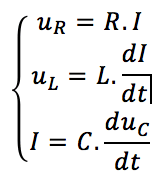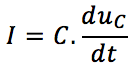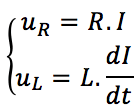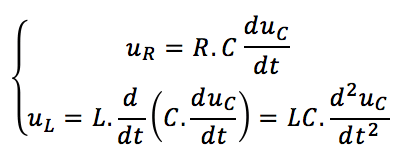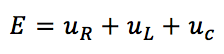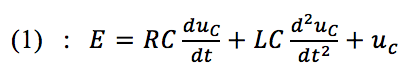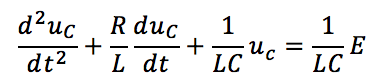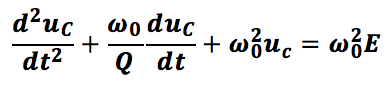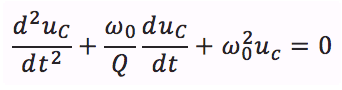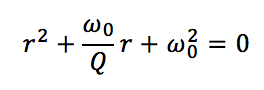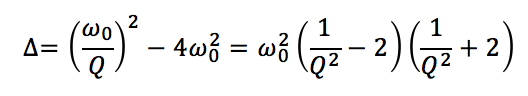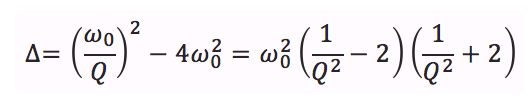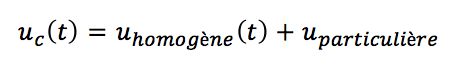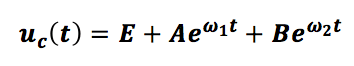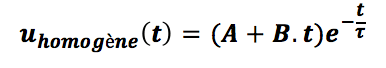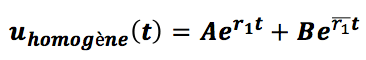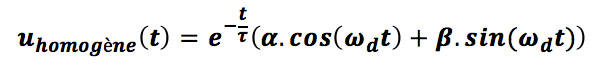Nous mettons en évidence dans cet article une « marche à suivre » applicable à la majorité des circuits de sup, en nous appuyant sur un exemple de circuit RLC.
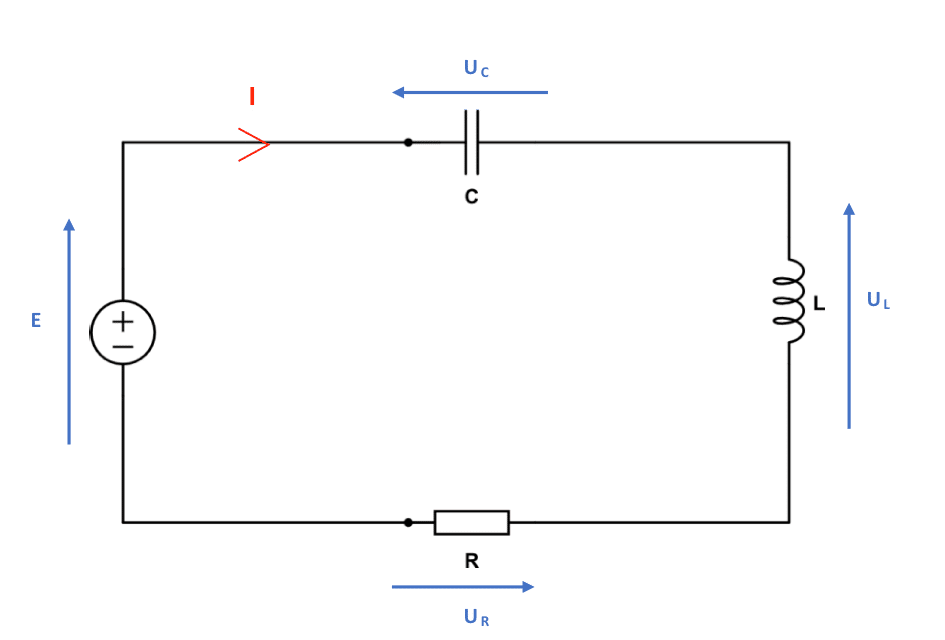
Exemple : le circuit RLC série
On commence bien évidemment par légender le circuit. Ici, nous nous sommes arrangés pour placer les tensions des dipôles en convention récepteur.
1. Ecrire les équations propres à chaque dipôle
2. Ecrire les lois des mailles et lois des nœuds
Nos dipôles étant ici en série, seule une loi des mailles sera pertinente :
3. Vérifier que l’on ait suffisamment d’équations pour résoudre le problème
Cela signifie tout simplement que si j’ai N inconnues dans mon problème, j’aurai besoin de N équations (linéairement indépendantes) portant sur ces inconnues afin de résoudre totalement mon système. Bien que des subtilités existent en algèbre, vous pouvez garder en mémoire ce principe en physique.
Dans notre exemple, les inconnues sont u_R,u_L,u_c et I. Nous disposons bien de 4 équations indépendantes, nous pouvons donc résoudre notre problème.
4. Observer la variable d’intérêt et la faire apparaître dans chaque équation
La variable à étudier va bien évidemment dépendre de ce que l’on vous demande, mais vous pouvez dans notre exemple trouver l’évolution de chacune des quatre variables.
Intéressons-nous pour illustrer notre propos à l’évolution de la tension u_c aux bornes du condensateur. L’équation de base à laquelle vous devez vous référer sera donc :
Cela nous permet de voir d’emblée, que l’intensité s’exprime simplement en fonction de notre variable. La variable u_c apparaissant déjà dans la loi des mailles, nous ne touchons pas à cette équation. Il nous reste donc à faire apparaître u_c dans les deux équations :
C’est ici assez trivial puisque l’intensité apparaît dans chacune d’entre elles. Elles se réécrivent ainsi :
5. Ecrire une équation différentielle portant sur la variable d’intérêt
Pour ce faire, on utilise simplement la dernière équation disponible :
Il vient ainsi:
6. Mettre l’équation différentielle sous forme canonique, mettre en évidence des grandeurs caractéristiques
Il faut tout simplement faire en sorte que le coefficient devant la dérivée de plus haut degré (ici (d^2 u_C)/(dt^2 )) valle 1. Ainsi dans notre équation (1), on divise tous nos termes par le produit LC, et l’on réordonne les dérivées par degré décroissant :
Que l’on réécrit finalement :
Où ω_0=1⁄√LC est la pulsation caractéristique et Q=1/R √(L⁄C) est appelé facteur de qualité.
7. Résoudre l’équation différentielle
La solution u_c (t) est la somme de la solution de l’équation homogène associée u_(homogène) et d’une solution particulière u_particulière. Le plus simple pour la solution particulière est de considérer une solution constante. En remplaçant cette solution constante dans notre équation, il vient immédiatement u_particulière=E. Résolvons maintenant l’équation homogène associée, i.e :
On commence par écrire le polynôme caractéristique :
que l’on résout en calculant le discriminant :
qui est donc du signe de (1/Q^2 -2). Trois types de régimes s’offrent alors potentiellement à nous :
a) ∆>0 : régime apériodique
Cela se produit lorsque Q>1⁄√2.
On a alors :
u_(homogène) (t)=Ae^(ω_1 t)+Be^(ω_2 t)
où ω_1 et ω_2 sont les deux racines du polynômes caractéristique. Il s’ensuit :
Les constantes A et B sont enfin à déterminer grâce aux conditions initiales, variables selon l’exercice.
b) ∆ =0∶régime critique
Cela se produit lorsque Q=1⁄√2
La solution est alors de la forme :
où A et B sont des constantes et τ un temps caractéristique (à exprimer en fonction de la racine double du polynôme caractéristique). Notez la présence du temps t dans le facteur devant l’exponentielle.
c) ∆<0∶régime pseudo-périodique
Cela se produit lorsque Q<1⁄√2.
Dans ce cas, les deux racines r_1 et r_2 du polynôme caractéristique sont complexes et conjuguées :
La solution s’écrit alors :
ce qui peut se retravailler sous la forme :