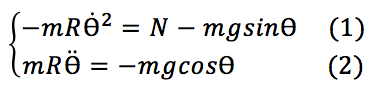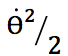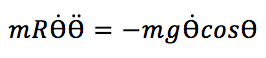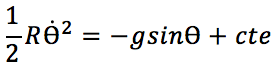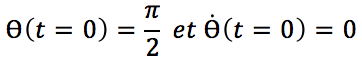Enoncé :
Un esquimau se laisse glisser du haut d’un igloo sans vitesse initiale. Quand décolle-t-il ?
Correction détaillée :
Nous sommes ici dans un cas typique d’exercice non guidé, pour lequel vous devez introduire vous-mêmes toutes les notations/grandeurs/coordonnées pertinentes.
Commençons évidemment par un schéma, en assimilant l’esquimau à un point matériel M de masse m, et l’igloo à une demie-sphère de centre O, de rayon R. Vue la géométrie du problème, on se place en deux dimensions et on utilise un système de coordonnées polaires (on peut également se placer en coordonnées sphériques à 3 dimensions, mais cela complexifiera pour rien le problème, des symétries rentrant en jeu).
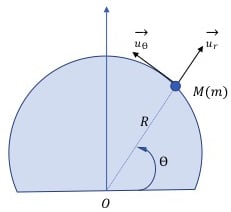
Commençons par un bilan des forces. La première remarque que nous pouvons faire est que la chute s’effectue sur la glace, surface au coefficient de frottement très faible. Il est donc raisonnable de supposer que la chute s’effectue sans frottements.
Partant de ce constat, seuls le poids et la réaction normale du support n’entrent en jeu.
Référentiel : Terrestre, supposé Galiléen
Système : l’esquimau M de masse m assimilé à un point matériel
Bilan des forces : le poids P et la réaction normale N de l’igloo
Avant d’écrire des équations, analysons le problème. Il s’agit de caractériser le « décollage » de l’esquimau. En d’autres termes, nous devons trouver un moyen d’exprimer une équation physique correspondant à la phrase « l’esquimau n’est plus en contact avec l’igloo ». Il s’agit évidemment d’indiquer que la réaction normale du support s’annule au décollage de l’esquimau :
L’esquimau est en contact avec l’igloo tant que N > 0
L’esquimau décolle dès que N=0
Exprimons nos forces dans notre base (les grandeurs en gras représentent des vecteurs) :
Exprimons également l’accélération de l’esquimau (à connaître par cœur) :
Appliquons le principe fondamental de la dynamique à l’esquimau :
En projection sur ur et uƟ ∶
Ces équations sont non linéaires, et mêlent des dérivées simples à des fonctions sinusoïdales. De manière générale, retenez bien les techniques qui suivent. Lorsque vous voyez :
- Du
→ essayez de dériver pour faire apparaître du 
: très souvent, les 
se simplifieront dans votre équation - Du
couplé à des fonctions sinusoïdales → multipliez votre équation par 
pour faire apparaître du facilement intégrable en 
→ essayez de dériver pour faire apparaître du 
: très souvent, les 
se simplifieront dans votre équation
couplé à des fonctions sinusoïdales → multipliez votre équation par 
pour faire apparaître du 
Nous utilisons tout d’abord le second point sur l’équation (2) :
On intègre et il vient :
Conditions initiales :
Finalement on obtient :
Et l’on réinjecte cette expression dans (1) pour obtenir l’expression de la réaction normale :
On conclut, en disant que l’esquimau décolle de l’igloo pour N = 0, soit pour :
L’exercice est alors résolu, mais nous pourrions poursuivre l’explication en déterminant par exemple sa vitesse d’envol, en caractérisant son mouvement ultérieur, etc … → à vous de jouer !