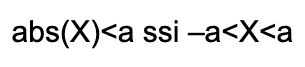Par Olivier Sarfati, professeur de maths et directeur de MyPrepa.
Cette année, le sujet de maths ECE 2019 présentait une forme assez standard : 3 exercices sur les 3 grandes parties du programme à savoir l’algèbre, l’analyse et les probabilités. Voyons les questions que l’on devait absolument traiter sur ce sujet. Vous trouverez à la fin de l’article des vidéos pour aller plus loin dans l’analyse ainsi qu’une correction sous format pdf. Si vous êtes en première année, nous vous conseillons d’essayer de réfléchir aux questions par vous-mêmes avant de regarder l’analyse d’Olivier puis de consulter la correction.
Exercice 1 : Algèbre linéaire
Chapitres concernés : Calcul matriciel, applications linéaires, diagonalisation, puissance n-ième de matrices
Niveau de difficulté : facile
On commence avec un exercice assez commun où la principale difficulté réside dans la compréhension du cours sur le rapport entre endomorphisme et matrices représentatives. Plus précisément, on pouvait vraiment s’amuser sur les questions suivantes :
Partie A)
Q1.a) easy.
Q1.b) on utilise le cours sur les polynômes annulateurs et on trouve bien 0 unique racine de X^3, ce qui répond à la question.
Q1.c) calcul.
Q1.d) sans doute la question qui tombe le plus aux concours en ECE : on fait une rapide démonstration par l’absurde : si f était diagonalisable, alors A serait diagonalisable et semblable à une matrice nulle. C’est absurde car alors A serait nulle… Plus simplement ici, on se resservait de la dimension du sous-espace propre associé à la valeur propre 0, c’est-à-dire Kerf, et c’était plié.
Q2.a) on montre la liberté de la famille qui est de longueur 3 (ou de cardinal 3) et comme dimE=3, on est bien en présence d’une base.
Q2.b) calcul.
Q3.a) on résout un système ou on le fait de tête. Dans tous les cas, on finit par y arriver si on est précis dans le calcul.
Q3.b) calcul
Q3.c) Question sympa qui se fait très rapidement si on a bien assimilé le cours. On montre en effet que M’ est inversible (peut-être est-elle triangulaire avec des éléments diagonaux non nuls ?) donc h est bijective et donc M est inversible. Souvenez-vous M’ et M représentent le même endomorphisme. Donc si l’une est inversible, l’autre l’est nécessairement…
Q3.d) C’est du calcul et on cherche une matrice B telle que MB=BM=I. Le B que l’on trouve n’est rien d’autre que la matrice M^(-1).
Q3.e) un classique sur le binôme de Newton.
Partie B) :
Q1) on se sert de V^2=T et ça vient tout seul. V représente g dans B’ et T représente f dans B’ donc on a directement gof=fog, d’après le cours.
Q2.a) on calcul fog(e1’), on trouve 0 d’où le résultat demandé. Comme e1’ est sans doute une base du noyau de f, on a également directement le résultat puisque g(e1’) appartient à Vect(e1’)…
Q2.b,c,d) dans le même esprit, on calcule et on finit par trouver.
Q3) on calcule encore et encore et on arrive sans doute à une contradiction du type a=0 et/ou b=0 et/ou c=0. A creuser sans trop avoir peur car c’est vraiment jouable.
Bilan de l’exercice 1 :
Rien de bien compliqué ici. Un exercice tout public donc qui demandait, comme souvent en algèbre, une bonne compréhension du cours et une bonne maîtrise calculatoire.
Exercice 2 : Analyse première et deuxième année.
Chapitres concernés : Etude de fonctions, suites, fonctions de deux variables, Scilab
Niveau de difficulté : intermédiaire voire difficile par endroit
On est un peu moins serein que dans l’exercice 1 car on a à la fois des fonctions de 2 variables qu’on a souvent mal digérées, et des suites de première année que les étudiants ont tendance à délaisser ! Voyons voir sur quelles questions on pouvait se défendre.
Partie A) :
Q1) question qui fait peur et qui en a sans doute laissé quelques-uns sans voix ! Si vous arrivez à vous figurer ce schéma en 3D, on voit qu’au point de coordonnées (1,1), il semblerait que ça vaille autour de 3. Un rapide calcul de f(1,1) montre effectivement que cela fait 3. Et on voit que tout autour les lignes de niveau sont supérieures à 3. On peut donc conjecturer que localement – ici on est sur l’ensemble [0,5 ; 1,5]x[0,5 ; 1,5] – f admet un minimum local au point (1,1) qui vaut 3. On va le démontrer rigoureusement par la suite donc ça valait le coup, si on ne visualisait pas la question, de traiter la suite et de revenir réfléchir dessus…
Q2) c’est du calcul qui permet, normalement, de retrouver la conjecture du 1. Et comme on nous donnait ici la valeur de la hessienne H, on pouvait gérer la Q2.d) sans avoir fait les questions précédentes. Partie B) :
On bascule sur de l’analyse de première année ECE, avec des études de fonctions et une suite définie de manière implicite. Les amoureux de l’histoire des concours auront peut-être reconnu quelques similitudes avec l’exercice 1 de l’EDHEC 1997 ECE, souvent donné en DS et concours blancs par les professeurs de prépa. Q1) une étude de fonction simple.
Q2) on utilise classiquement le théorème de la bijection en n’oubliant pas de mentionner la continuité et la stricte monotonie de hn sur les deux intervalles.
Q3.a) calcul
Q3.b) calcul aussi.
Q3.c) un grand classique sur les suites implicites. On remarque simplement que hn+1(vn+1)=4 et donc l’inégalité 3.b) devient hn+1(vn)>hn+1(vn+1). Et comme hn+1 est croissante sur [1,+l’infini[, on a vn>vn+1 : CQFD !
Q4.a) on utilise le théorème de la limite monotone : v est décroissante minorée par 1 donc converge vers un réel l, et par prolongement des inégalités, on a l supérieur ou égal à 1.
Q4.b,c) on montre par l’absurde que l vaut finalement 1 mais ce n’est pas si simple… Plus de précisions dans notre vidéo.
Q5) du Scilab pour finir, où des points sont à aller chercher mais ce n’était pas facile. On fait une étude dichotomique sur l’intervalle [1 ; 3] dont je rappelle le principe dans la vidéo (compliqué sur un article !). En 5.d), on voit que le programme calcule (vn)^n et que, selon le graphique, cette valeur serait égale à environ 2,6. On le démontre ensuite en Q5.e)
non sans mal : il fallait penser à faire apparaître judicieusement un trinôme du second degré : visionnez la vidéo pour en savoir plus. Et on est rassurés : quand on prend une calculatrice, on trouve (vn)^n=2,62.
La Q5.f) était jouable mais finalement assez délicate… Il fallait avoir l’idée de passer à la forme exponentielle pour s’en sortir…
Bilan de l’exercice 2 :
Un exercice qui a dû ravir les étudiants qui avaient bien revu le chapitre de première année mais qui a dû désarçonner les autres. Quelques questions délicates toutefois donc un exercice parfait pour préparer la BCE !
Exercice 3 : Probabilités et analyse
Chapitres concernés : intégrales impropres, variables à densité, variables aléatoires discrètes, Scilab
Niveau de difficulté : intermédiaire
On finit par un exercice où il va falloir être bon sur le calcul intégral ! Zoomons sur quelques questions.
Partie A) :
Q1) rien à signaler.
Q2) on reconnaît une intégrale de Riemann facile à calculer.
Q3.a) du changement de variable sans trop de complexité.
Q3.b) la réponse vient rapidement par la relation de Chasles.
Q4.a,b,c) on se sert de la densité et on fait du calcul. Idem pour l’espérance et la variance. Rien à signaler.
Q5) Là, on doit bien maîtriser ses classiques sur la valeur absolue.
Pour rappel :
Et ensuite tout en découle sans trop souffrir.
Partie B)
Q1.a) un cadeau car en analysant le support, on trouve une loi de Bernoulli de paramètre ½.
Q1.b) D et Y étant indépendante, on peut calculer l’espérance de T en utilisant E(D) et E(Y).
Q1.c) Il fallait ici penser à faire une formule des probabilités totales. Visionnez la vidéo pour en savoir plus.
Q2) du calcul qui semble très abordable.
Q3) Une simulation Scilab pour finir. A faire s’il vous reste du temps.
Bilan de l’exercice 3:
Un exercice très calculatoire mais où les calculs ne semblent pas très complexes. A faire donc pour s’entraîner sur les densités avant la BCE !
Conclusion :
Un sujet assez complet avec des passages très simples, d’autres plus compliqués voire très compliqués pour des ECE (exercice 2). Un sujet qui devrait permettre de bien échelonner les notes des candidats et qui démontre une fois de plus l’importance de passer les concours Ecricome, y compris lorsqu’on ne vise que le top 5, car le concours est une super révision des concours BCE.
Retrouvez ci-dessous la correction du sujet par Frédéric Brossard, professeur de Maths chez MyPrepa :