Olivier Sarfati, professeur de maths et directeur de MyPrepa, nous livre son analyse
Sujet Maths ECS EMLyon du concours BCE 2019
Analyse du sujet
Généralement, on retrouve deux types de sujet EML : les sujets qui présentent deux problèmes, et ceux qui n’en présente qu’un. Cette année, les concepteurs ont choisi la seconde option : un long problème découpé en 5 parties relativement indépendantes. A première vue, on est content car on reconnaît beaucoup de questions classiques autour du théorème fondamental de l’analyse (intégration sur un segment) mais on est quelque peu sidéré par la longueur inhabituelle du sujet. Il va falloir, comme souvent, être concis, précis et rapide, très rapide. Voyons ensemble les grands classiques qui semblaient vraiment incontournables et que je vais illustrer dans la vidéo tournée depuis notre plateforme de cours en ligne.
Au fil du sujet, vous pourrez visionner la correction vidéo avec les analyses, conseils et corrections d’Olivier Sarfati. Vous pouvez également télécharger le compte-rendu écrit :
Retrouvez également la correction écrite du sujet EMLyon ECS 2019 réalisée par M.BROSSARD professeurs de maths à Intégrale Prépa et MyPrepa :
Dans un premier temps, voici le sujet BCE EMlyon 2019 pour la section ECS. Vous trouverez l’analyse écrite de cette épreuve à la suite des sujets.


Partie A)
On commence par une partie qui ressemble à des sujets classiques qui ont traversé l’histoire des concours : ESSEC 1984 S, ESSEC 2002 E… mais en bien plus simple car on ne touche pas frontalement Phi_a dans cette partie.
Tout est simple et, si mes calculs rapides sont justes, les valeurs propres sont 2, 3,… k+2, … n+2. Et E_(k+2)=Vect(Q_k). Seule la question 4.d) demandait un peu de recul.
Partie B)
Q5.a) on utilise le théorème fondamentale de l’analyse. Easy donc.
Q5.b) Il fallait se souvenir ici qu’une fonction continue sur un intervalle est bornée… La croissance de l’intégration fait le reste.
Q5.c) une question qui demande un peu de soin pour bien encadrer sans faire n’importe quoi.
Q5.d) Se faisait sans doute par analogie avec ce qui précède mais attention à la croissance de l’intégration car cette fois x est négatif et donc les bornes ne sont plus dans l’ordre croissant…
Q6) la continuité se déduit de la question précédente. Pour la dérivation, on utilise encore le théorème fondamental.
Q7.a) le changement de variable u=-t doit faire l’affaire, comme dans l’ESSEC 2003 par exemple.
Q7.b) Du classique ici mais attention encore aux bornes qui ne sont pas nécessairement dans l’ordre croissant…
Q8) pas classique mais ne semble pas non plus très compliqué…
Partie C)
Q9) encore de la croissance de l’intégration avec les bornes à mettre dans le bon sens.
Q10) rien de nouveau depuis la partie B…
Q11) Une question délicate mais très sympa puisqu’elle exige des prises d’initiatives et une réutilisation de la question 8 de la partie précédente. A voir sur la vidéo pour le détail car ce n’était pas facile à trouver.
Q12) On revient sur des choses plus calculatoires : à faire car il y avait des points à prendre ici sans trop souffrir.
Partie D)
Q13.a) Une question classique que l’on donne souvent en première année. Une bonne maîtrise du cours sur les valeurs absolues nous permet de voir rapidement des identités remarquables…
Q13.b) on utilise la 13.a puis, par construction de E_2 et utilisation du critère de comparaison, on trouve la réponse.
Q14) et Q15) A faire absolument bien sûr.
Q16) ça ne ressemble pas à grand-chose et on sent que l’on va devoir faire pas mal de calcul. Les résultats sont tous donnés donc il fallait tenter car cela ne semble pas très complexe. Et on a l’occasion d’appliquer l’inégalité de Cauchy-Schwarz, ce qui est toujours un plaisir !
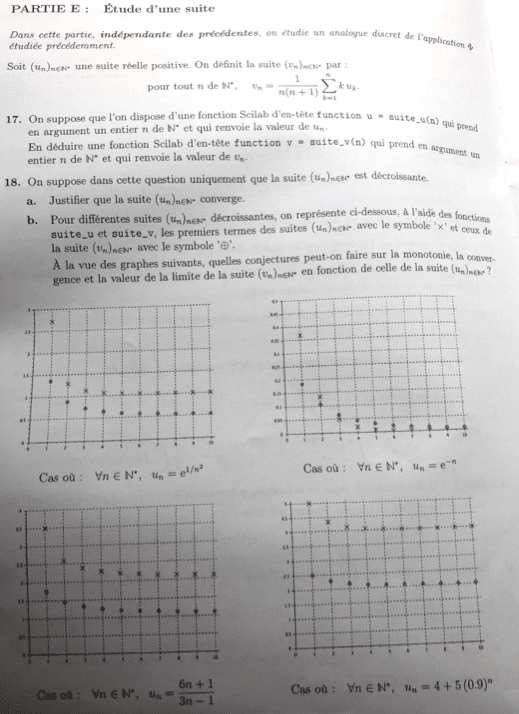
Partie E)
La partie la moins classique du sujet.
Q18.a) un cadeau puisque la suite est décroissante et minorée par 0…
Q18.b) même sans maîtriser Scilab, la question était abordable : il suffisait de lire le graphique…
Q18.c) la première inégalité est très simple puisque u est décroissante. On procède alors par encadrement et on retrouve la somme des k qui fait n(n+1)/2…
Pour la seconde inégalité, cela semble beaucoup plus casse-tête mais en analysant finement la réponse, les idées viennent. Une belle question pour faire la différence par rapport aux autres candidats. La réponse en vidéo.
Q18.d) calcul standard.
Q18.e) une sous-question qui conclut magnifiquement la question. Il s’agissait ici de montrer que v décroît, converge vers la moitié de la limite de la suite u. A voir en vidéo.
Q19.a) calcul.
Q19.b) il ne fallait pas oublier ici que la suite des sommes partielles est une suite ! On montrait ici que la suite des sommes partielles de la série de terme général v_n était croissante majorée. A savoir refaire car ce type de technique tombe souvent aux concours.
Q19.c) un joli raisonnement par l’absurde où l’on rejoint une série de Riemann dans le cas divergent… Très sympa.
Q19.d) déduction logique de ce qui précède.
Q20.a) En n’oubliant pas qu’en sommant une variable aléatoire sur son univers, on obtient 1, le résultat venait aisément.
Q20.b) on termine encore avec des équivalents et un critère d’équivalence de séries à termes positifs dans le cas divergent.
Conclusion
Un problème long mais assez intéressant et qui demande de la finesse dans la conduite des raisonnements et des calculs. Les parties étant relativement indépendantes, le sujet est un bon problème de révision.
Téléchargez le compte rendu du corrigé du sujet EMLyon ECS réalisé par Olivier Sarfati :
Vous pouvez également consulter les autres corrigés et analyses réalisés par l’équipe MyPrepa :
BCE:
Le Concours Corrigé : Analyse du sujet Maths 1 ECS HEC ESSEC BCE 2019
Le Concours Corrigé : Analyse du sujet Maths 2 ECS HEC ESCP BCE 2019
Ecricome:
Le Concours Corrigé : Analyse Ecricome HGG sur la Chine 2019
Le Concours Corrigé : Analyse Ecricome Culture générale 2019
Le Concours Corrigé : Analyse Ecricome Maths ECE 2019
Le Concours Corrigé : Analyse Ecricome Maths ECS 2019





