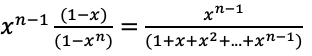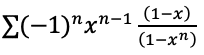Le Concours Corrigé : Analyse du sujet CCINP 2019 – MP épreuve 1

CCINP MP 1 2019

Par Louis-Thibault Gauthier, professeur de Maths chez MyPrepa

Cette épreuve est assez courte et les questions sont d’un niveau assez élevé à partir de l’exercice 2. Ce sujet aborde les probabilités et les séries de fonctions. Voyons ensemble comment il fallait procéder.

Voici le sujet de l’épreuve 1 MP du concours commun CCINP :

Exercice 1

1) Question facile et très classique. Pour l’intégrabilité de f : f est continue sur l’intervalle ouvert sur lequel on l’intègre, et est prolongeable par continuité en 0 en posant f(0)=1 (faire un DL). En + l’infini, f est un o(1/t^2) par croissances comparées.

Pour l’intégrale à calculer, multipliez en haut et en bas par e^{-t}, puis décomposez 1/(1-exp(-t)) en somme d’une série géométrique de raison différente de 1. Utilisez le théorème d’interversion série/intégrale.
Pour calculer l’intégrale suivante :
effectuez le changement de variable u=(n+1)t.

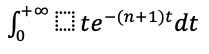
Exercice 2

2) Comparaison avec la série ∑p_n qui est convergente de somme 1. Ensuite pour la première méthode, il faut commencer par décomposer .
La deuxième méthode est une application directe de l’indépendance de t_X1et de t_X2, qui est entraînée par l’indépendance X1 et X2. 3) Il convient de factoriser On développe grâce à la formule du binôme de Newton et on identifie ce polynôme en t avec la définition de la fonction génératrice de S_n, pour en déduire la loi.

Problème

4) Ceci est équivalent à 1 car xⁿ tend vers 0 quand n tend vers l’infini. On peut prendre comme exemple la suite de terme général 1/(n+1)^2 qui va converger pour x=2.
5) La convergence normale implique la convergence uniforme.
6) Utilisez le théorème de dérivation de la somme d’une série de fonctions. Pour la convergence uniforme de la somme des f’n sur tout segment de ]-1,1[, copiez le raisonnement de la 5.
7)La première partie revient à montrer que l’ensemble des (In) pour n un entier naturel non nul forme une partition de A. Utilisez ensuite le théorème de sommation par paquets.
8) Application de la question 7).
9) 1 ≤ a_n ≤ n, donc on utilise le théorème de comparaison des rayons de convergence des séries entières.
10) Utilisez le critère spécial des séries alternées puis le théorème de la double limite.
11) Le théorème de la double limite donne que cette limite vaut -1. Donc un équivalent en 0 de f(x) est -x.
12) Décomposez par la somme « inversée » de la somme des termes d’une suite géométrique. Puis majorez cette expression brutalement par 1/n, car tous les x^i sont plus grands que x^(n-1) (car x est entre 0 et 1). Ceci afin de montrer la convergence uniforme de .Cela nous permet d’appliquer à nouveau le théorème de la double limite